K-means from scratch

A step-by-step walkthrough of a simple clustering algorithm

Julia

Clustering

Author

Simon Steiger

Published

November 2, 2023

In a nutshell

This is my attempt at coding \(K\)-means from scratch. I have used the pseudocode from this handout on AI systems as a starting point but so far not looked into optimized solutions. I can already think of a few improvements which would affect efficiency though, so this version is certainly clunkier and slower than necessary. 🐢

Let’s begin by describing the goal of \(K\)-means mathematically.

\[ \text{minimize} \ \sum_{i=1}^n \| \mathbf{x}_i - \boldsymbol{\mu}_{z_i} \|^2 \ \text{w.r.t.} \ (\boldsymbol{\mu}, z) \]

In this equation, \(\boldsymbol{\mu}_k\) is the center of the \(k\)-th cluster, and \(z_i\) is an index of the cluster for \(i\)-th point \(\mathbf{x}_i\). I have also seen \(K\)-means being described as a coordinate-descent algorithm, but I am not yet deep enough into the terminology to understand that well.

Coding K-means

I will start by laying out the general structure of the algorithm and then defining its components one by one.

Main function

function kmeans(k, X; max_iter=1000, seed=42)
    
    # Dimensionality of the problem
    nfeatures, nobs = size(X)

    # Initialize random centroids and empty label vector
    initctr = initcentroids(nfeatures, k; seed)
    initlbl = Vector{Int64}(undef, nobs)

    # Track the state of the algorithm
    state = KmeansResult(k, X, initctr, initlbl, 0, seed, [], [])
    
    # Minimize Euclidean distance until convergence or maximum iterations
    while notconverged(state.log_centroids, state.iter, max_iter)

        # Assign labels to each observation based on centroid location
        assign!(state.labels, X, state.centroids)
        push!(state.log_labels, copy(state.labels))

        # Reposition centroids based on assigned observations
        reposition!(state.centroids, X, state.labels, k, state.iter)
        push!(state.log_centroids, copy(state.centroids))

        # Increment iteration counter
        state.iter += 1
    end

    # Warn if no convergence after reaching iteration limit
    state.iter == max_iter && @warn "Did not converge after $max_iter iterations."
    
    return state
end;

Helper functions

Now that we’ve laid out the general logic we want the \(K\)-means algorithm to follow, we still need to craft a few tools to make it run.

First up is an object class (called a struct in Julia), which will allow us to track all relevant parameters of the algorithm in a single place. This will also be the result that is returned to the user.

In detail, we’ll track and return the following:

k, the number of clusters to be fit
X, the matrix of the data to be clustered
centroids, the final centroids of the clusters
labels, the final labels of the observations
iter, the number of iterations until the algorithm ended
seed, the random seed used for cluster initialization
log_centroids, a vector of centroid-matrices, for each iteration one matrix
log_labels, a vector of label-vectors, for each iteration one vector

mutable struct KmeansResult
    k::Int64
    X::Matrix{Float64}
    centroids::Matrix{Float64}
    labels::Vector{Int64}
    iter::Int64
    seed::Int64
    log_centroids::AbstractArray
    log_labels::AbstractArray
end

Why mutable struct?

Unlike mutable structs, pure structs are immutable after creation, meaning that the values stored in each field cannot be altered. The pure version would be a poor choice in our case, since we want to update the state of the algorithm at each iteration step. Therefore, we need a mutable struct. This type is generally less memory efficient and comes with reduced performance, but we can’t avoid it here (I think)!

Initializing centroids

First, we need a function which initializes random centroids at the beginning of the algorithm (but it’s also very useful as a reboot when one of our centroids ends up without any observations assigned to it! 🤫).

We’ll use the Xoshiro256++ pseudorandom number generator to manually set random seeds for initial centroids.

import Random: Xoshiro

initcentroids(d, k; seed=42) = randn(Xoshiro(seed), d, k);

Checking convergence

We need a function which determines if the \(K\)-means algorithm has converged, or if it has reached the maximum number of iterations.

During each iteration, this function checks for three conditions.

1. First iteration

The algorithm cannot converge during the first iteration (itr < 2) because we define convergence as the absence of change in centroids between two consecutive evaluations. Hence, we need a second iteration to evaluate convergence.

2. Static centroids

I’ve already mentioned the second condition, which is that there is no change in centroids between two consecutive iterations. Since we want the condition to evaluate to false, we have to flip it and get ctr[itr] ≠ ctr[itr-1].

3. Maximum iterations

Finally, the algorithm should stop once it has reached the maximum number of iterations (itr < max).

notconverged(ctr, itr, max) = (itr < 2 || ctr[itr] != ctr[itr-1]) && itr < max;

Looking at the boolean algebra connecting these three conditions in the function above, we see that the algorithm will stop, i.e., notconverged() will return false, when both condition 1 and 2 evaluate to false, or when condition 3 evaluates to false.

Calculating distances

The \(K\)-means algorithm uses Euclidean distances between the vector of the centroid(s) and each observation. We’ll use a version of the formula which generalizes to higher dimensions.

\[ \Delta(p,q)={\sqrt {(p-q)^{2}}} \]

euclidean(x, y) = √(sum((x .- y) .^ 2));

As it stands, this function will work well for calculating the distance between two vectors. What we really need though are pairwise distances between two sets of vectors, one being the observations and the other one being the centroids.

To help with this, I’ll define a helper which makes the euclidean() function work as described.

function pairwise(f, x, y; dims=1)
    [f(i, j) for i in eachslice(x, dims=dims), j in eachslice(y, dims=dims)]
end;

Assigning labels

We label each observation depending on which centroids it’s closest to in Euclidean space.

This function could be improved because it is inefficient¹ and could be prettier ².

function assign!(lab, X, ctr)
    Δ = pairwise(euclidean, X, ctr, dims=2)
    idxmin = findmin(Δ, dims=2)[2]
    [lab[i] = idxmin[i][2] for i in eachindex(idxmin)]
end;

Repositioning centroids

In each iteration, we want to reposition the centroids to the means of the observations assigned to them.

This concept breaks down if one of the centroids is assigned no observations at all. In this scenario, we will reinitiate that centroid randomly and move to the next iteration.

import StatsBase: mean

function reposition!(c_new, X, labels, k, iter)
    for i in 1:k
        idx = labels .== i
        if all(!, idx)
            c_new[:, i] = initcentroids(size(c_new, 1), 1; seed=iter)
        else
            c_new[:, i] = [mean(r) for r in eachslice(X[:, idx], dims=1)]
        end
    end
end;

Want a different random centroid?

We’ll have to use a different seed than the one initcentroids() uses by default! Otherwise, we would initiate a new centroid in exactly the same position as the one that failed us before. I have chosen to set the seed to iter, so even if the reinitiation fails repeatedly, the algorithm will try with a new centroid each time. Finally, if it never succeeds, the algorithm still stops at upon reaching the maximum number of iterations.

Standardising features

Features passed to \(K\)-means must be standardised.

standardise(x) = (x .- mean(x)) ./ std(x);

So far so good! I think that’s all we need.

Simulating clusters

… before we can take our freshly baked \(K\)-means algorithm out for a spin, we first need to cook up some data to play with. We will draw this data from a mixture of gaussians.

You can customize the data-generating process regarding (as soon as I figure out how to hook up Pluto here)

The number of generated samples
The separation of the clusters
The number of clusters

Let’s write down the recipe for this mixture of gaussians!

using Distributions, LinearAlgebra

function generate_multivariate_data(n, κ, separation; seed=42)
    # Pass seed to random number generator
    rng = Xoshiro(seed)

    # Samples are equally likely to belong to any of the clusters
    probvec = fill(1/κ, κ)
    switch = Categorical(probvec)

    # Create a Multivariate Normal with κ clusters (μ) and covariance Σ
    gaussians = map(1:κ) do idx
        angle = 2π / κ * (idx - 1)
        bas_v = separation * [1.0, 0.0]
        R     = [cos(angle) -sin(angle); sin(angle) cos(angle)]
        μ     = R * bas_v
        Σ     = Matrix(Hermitian(R * [10.0 0.0; 0.0 20.0] * R'))
        return MvNormal(μ, Σ)
    end

    # Sample true cluster membership of each observation from Categorical
    z = rand(rng, switch, n)
    
    # Initialise a vector to store the result
    y = Vector{Vector{Float64}}(undef, n)

    # Sample from Multivariate Normal
    for i in 1:n
        y[i] = rand(rng, gaussians[z[i]])
    end

    return y
end;

Inspecting the data

~~Play around with the sliders to set the sample size, number of clusters, and cluster separation.~~ Then we’ll use this data to test our new \(K\)-means algorithm!

using StatsPlots

X = reduce(hcat, generate_multivariate_data(3000, 4, 10))

histogram2d(X[1, :], X[2, :], bins=50)

What does the input to separation do?

If you pay attention to the axes, you’ll realize that this parameter simply stretches out the space in which the gaussians are located, thus pulling them apart or moving them closer together.

Proving ground

Time to try our new \(K\)-means algorithm!

We first need to standardise the input matrix.

Z = standardise(X)

And action!

We will fit five clusters to this data and set a seed.

k = 6;
seed = 42;

Time to fit!

fit = kmeans(k, Z, seed=seed);

We can inspect the result by looking at the different fields of fit. To check the final centroids, we would do the following:

fit.centroids

Tracking K-means

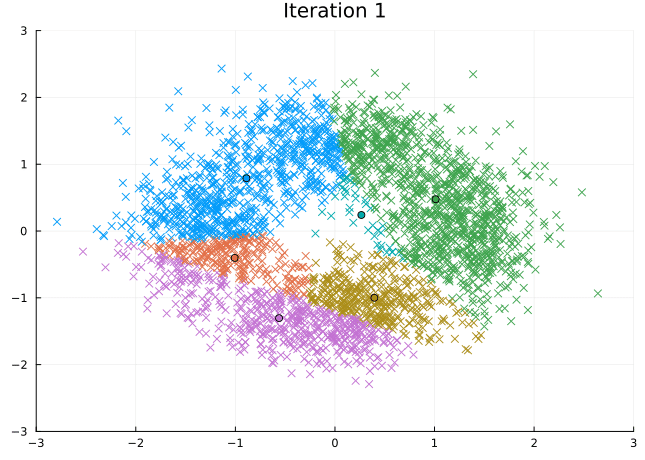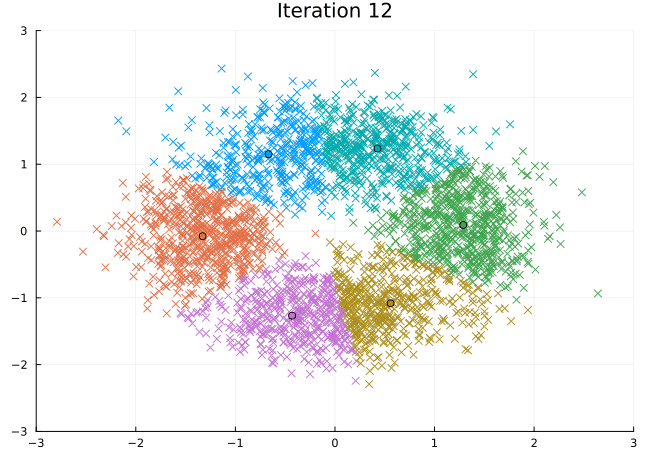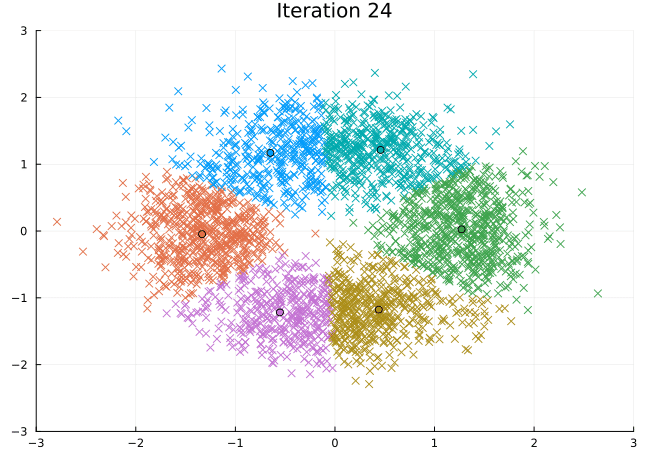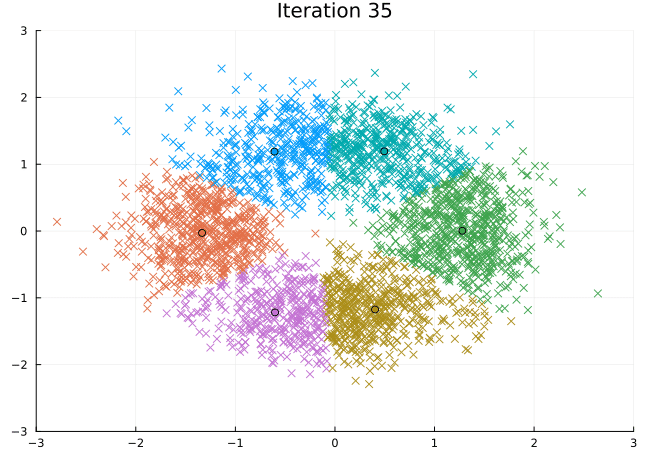
Let’s look at the steps the \(K\)-means algorithm takes to find its solution.

@gif for i in eachindex(fit.log_centroids)
    scatter(Z[1, :], Z[2, :], c=fit.log_labels[i], markershape=:xcross, legend=:none)
    scatter!(fit.log_centroids[i][1, :], fit.log_centroids[i][2, :], c=[1:k;])
    title!("Iteration $i")
    xlims!(-3, 3), ylims!(-3, 3)
end every 1 fps=15

Footnotes

🐢 This is currently updating the labels indiscriminately without checking if the centroid has changed at all.↩︎
🪳 I don’t like the way I’m accessing the CartesianIndices returned by findmin(). There is probably a better solution with view().↩︎